Vue浅拷贝和深拷贝
前言
在理解浅拷贝和深拷贝浅前,必须先理解基本数据类型和引用数据类型的区别。
一、数据类型
1.1.基本数据类型
字符串(Sring)、布尔值(Boolean)和数字(Number)
1.2.引用数据类型
数组(Array)和对象(Object)
1.3.区别
基本数据类型是存储在栈内存中。而引用类型存放的值是指向数据的引用,而不是数据本身,真实数据是存放在堆内存里,具体见如下:
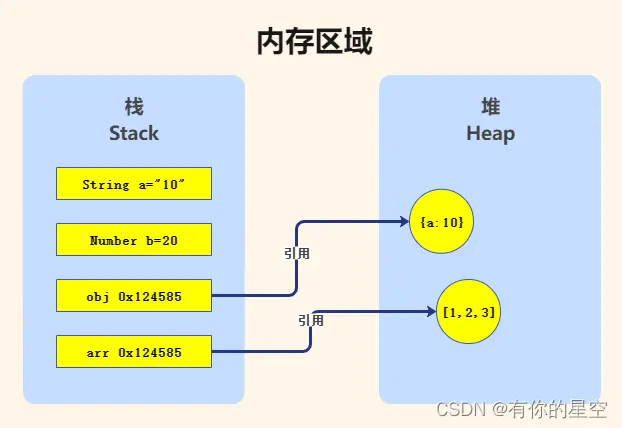
二、浅拷贝
2.1. 定义
浅拷贝是按位拷贝对象,它会创建一个新对象,这个对象有着原始对象属性值的一份精确拷贝。如果属性是基本类型,拷贝的就是基本类型的值;如果属性是内存地址(引用类型),拷贝的就是内存地址 ,因此如果其中一个对象改变了这个地址,就会影响到另一个对象。即默认拷贝构造函数只是对对象进行浅拷贝复制(逐个成员依次拷贝),即只复制对象空间而不复制资源。
2.2. 浅拷贝特点
对于基本数据类型的成员对象,因为基础数据类型是值传递的,所以是直接将属性值赋值给新的对象。基础类型的拷贝,其中一个对象修改该值,不会影响另外一个。
var a = 10
var b = a
b = 20
console.log("a",a) //10
console.log("b",b) //20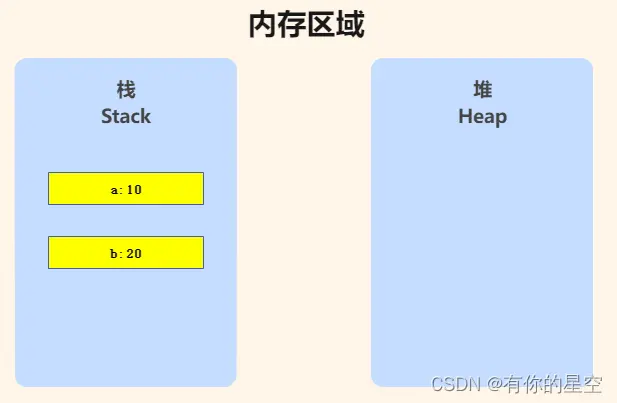
对于引用类型,比如数组或者类对象,因为引用类型是引用传递,所以浅拷贝只是把内存地址赋值给了成员变量,它们指向了同一内存空间。改变其中一个,会对另外一个也产生影响
var obj = {
a:"AAA"
}
var obj2 = obj
obj2.a = "BBB"
console.log("obj",obj) //{name: "BBB"}
console.log("obj2",obj2) //{name: "BBB"}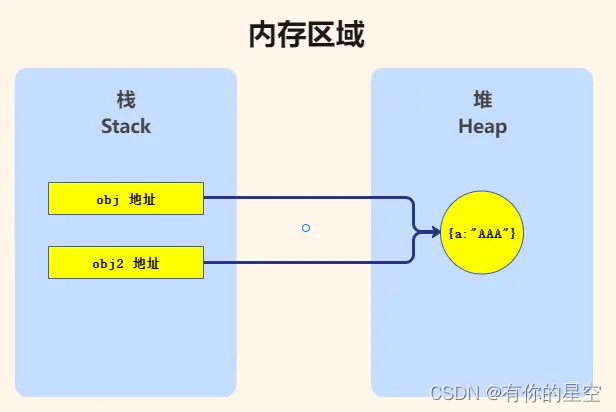
三、深拷贝
3.1. 定义
深拷贝,在拷贝引用类型成员变量时,为引用类型的数据成员另辟了一个独立的内存空间,实现真正内容上的拷贝。
3.2. 深拷贝特点
对于基本数据类型的成员对象,因为基础数据类型是值传递的,所以是直接将属性值赋值给新的对象。基础类型的拷贝,其中一个对象修改该值,不会影响另外一个(和浅拷贝一样)。
对于引用类型,比如数组或者类对象,深拷贝会新建一个对象空间,然后拷贝里面的内容,所以它们指向了不同的内存空间。改变其中一个,不会对另外一个也产生影响。
var obj = {
a:"AAA"
}
var obj2 = {} // 创建新的对象
obj2 = obj
obj2.a = "BBB"
console.log("obj",obj) //{name: "AAA"}
console.log("obj2",obj2) //{name: "BBB"}
四、拷贝实现方案
4.1. Object.assign()
单级结构时深拷贝,多级结构浅拷贝,Object.assign()对象是用于将所有可枚举属性的值从一个或多个源对象复制到目标对象,将返回目标对象。
a)单级结构(一级拷贝是深拷贝):
var obj = {
a: 10,
}
var obj2 = Object.assign({}, obj);
obj2.a = 20
console.log("obj",obj); //{a: 10}
console.log("obj2",obj2) //{a: 20}b)多级结构(一级拷贝是浅拷贝,修改二级对象还是会影响原对象):
var obj = {
a: 10,
b: {
c:"AAA",
d:666
}
}
var obj2 = Object.assign({}, obj);
obj2.b.c = "BBB"
console.log("obj",obj); //{a: 10,b: {c:"BBB",d:666}}
console.log("obj2",obj2); //{a: 10,b: {c:"BBB",d:666}}4.2. concat()
单级结构时深拷贝,多级结构浅拷贝
a)单级结构(一级拷贝是深拷贝):
let arr = [1, 2];
let arr2 = arr.concat();
arr2[1] = 3;
console.log("arr",arr) //[1, 2]
console.log("arr2",arr2) //[1, 3]b)多级结构(一级拷贝是浅拷贝):
let arr = [1, 2, {
a: 'AAA'
}];
let arr2 = arr.concat();
arr2[2].a = 'BBB';
console.log("arr",arr) //[1, 2, {a: 'BBB'}]
console.log("arr2",arr2) //[1, 2, {a: 'BBB'}]4.3. slice()
单级结构时深拷贝,多级结构浅拷贝
a)单级结构(一级拷贝是深拷贝):
let arr = [1, 2, 3];
let arr2 = arr.slice();
arr2[1] = 4;
console.log("arr",arr) //[1, 2, 3]
console.log("arr2",arr2) //[1, 4, 3]b)多级结构(一级拷贝是浅拷贝):
let arr = [1, 2, {a:'AAA'}];
let arr2 = arr.slice();
arr2[2].a = 'BBB';
console.log("arr",arr) //[1, 2, {a: 'BBB'}]
console.log("arr2",arr2) //[1, 2, {a: 'BBB'}]4.4.JSON.parse(JSON.stringify())
用JSON.stringify将对象转成JSON字符串,再用JSON.parse()把字符串解析成对象,一去一来,新的对象产生了,而且对象会开辟新的栈,实现深拷贝。
单级多级均为深拷贝,但需要注意无法拷贝RegExp对象、function和symbol
let arr = [1, 2, {a:'AAA'}];
let arr2 = JSON.parse(JSON.stringify(arr))
arr2[2].a = 'BBB';
console.log("arr",arr) //[1, 2, {a: 'AAA'}]
console.log("arr2",arr2) //[1, 2, {a: 'BBB'}]4.5. cloneDeep()
单级多级均为深拷贝,使用lodash工具中cloneDeep方法实现深拷贝,需要通过npm引入lodash库
npm i -save lodash //全局安装<script>
import _ from 'lodash';
export default {
name: 'Test',
mounted() {
const arr = [1, 2, { a: 'AAA' }];
const arr2 = _.cloneDeep(arr);
arr2[2].a = 'BBB';
console.log('arr', arr); // [1, 2, {a: 'AAA'}]
console.log('arr2', arr2); // [1, 2, {a: 'BBB'}]
},
};
</script>五、结论
| 类型 | 第一级为基础数据类型 | 原数据中包含子对象 |
|---|---|---|
| 浅拷贝 | 改变不会使原始数据改变 | 改变会使原始数据改变 |
| 深拷贝 | 改变不会使原始数据改变 | 改变不会使原始数据改变 |
原文链接:https://blog.csdn.net/ltlt654321/article/details/127047262
0 人喜欢
暂无评论,来发布第一条评论吧!

