元素周期表中,竟然还有一个不为人知的神秘元素?
一提到化学,可能大部分人脑海里都会自动出现一连串令人眼花缭乱的复杂方程式,甚至“谈化学色变”。其实,化学并没有这么可怕,它距离我们的日常生活也非常近。从我们每天吸入的氧气和呼出的二氧化碳、“多喝热水”和泡脚养生,到佩戴的各种饰品、驾驶或乘坐的各种交通工具等等,都有化学的“踪迹”。可以说,物质世界就是由化学元素所构成的。
自1869年俄国著名化学家门捷列夫提出元素周期律以来,现包括天然元素及人造元素,已有记录元素共计118个。当科学家们反复审视这张元素周期表时,也更多地开始思考,是否存在一个神秘的0号元素呢?
从原子的结构说起
中学时期,我们就曾经学过,原子由原子核和核外电子组成,是化学反应中的最小单位。其中,原子核由质子和中子通过强相互作用力(质子和中子间独有的吸引力)结合组成。
质子的个数直接关系到元素本身的化学性质,原子核中的质子个数则是区分元素种类的重要标志。相同质子数代表着同种元素,相同质子数和中子数的元素称为一种核素,相同质子数不同中子数的元素互称为同位素。
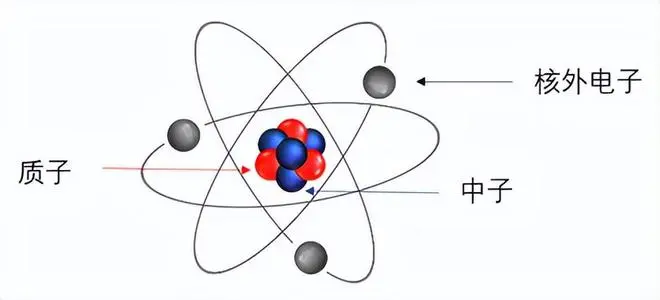
被人熟知的1号元素——氢元素
相信大家对于元素周期表中的1号元素——氢元素,都并不陌生。在自然界中,氢元素含量丰富。人类生活必需的水,就是由氢元素和氧元素两种元素所组成的。
在氢核素中丰度最高的是仅由一个质子和一个核外电子组成的1H,此外再添加一个中子就得到了同位素氘2H,氘是氢弹的主要原材料。由于1H原子核中没有中子的存在,因此当1H原子失去核外电子时,氢离子也就等同于游离的质子。当大量氢离子存在于水中,水溶液便会产生酸性,这便是酸在水中电离的过程。
举个例子,我们都知道的是,很多酸具有强腐蚀性,就算是生活中常见的调味料食醋,也可以和水垢、铁钉等发生化学反应,这就是质子化学性质最基本的体现。
0号元素真的存在吗?
乍听0号元素,很多人可能会一头雾水。化学书上写的不是“氢氦锂铍硼,碳氮氧氟氖”吗?难道是我的记忆出现了混乱?不用慌!其实,元素周期表里也没有0号元素。那么,这个神秘的0号元素究竟是个啥?
元素周期表中没有,并不代表0号元素就不存在。既然没有中子的质子可以单独作为一个元素,那么没有质子的中子为什么不可以呢?质子个数不同代表着元素种类的不同,那么,没有质子的元素,即0号元素,也被称为中子元素。
早在20世纪初,物理学家安德罗波夫就将自由中子命名为“0号元素”,并将其置于元素周期表中起始位——氦元素的正上方,意为质子数量最少的元素,并用符号Nu表示。
不过,除了少数讨论核素或同位素的情况外,其他情况下并不将0号元素列入元素周期表内。因此,我们在元素周期表中没见过0号元素,也很正常。

衰老的恒星促成0号元素的诞生
0号元素源于恒星的衰老过程,衰老的恒星自身坍塌时会造成极大的压力,将氢元素核外电子压入质子内部,从而形成电中性的中子粒子。其结构并不稳定,自由的中子半衰期只有十分钟左右,在常压环境下,会重新变成质子并释放反电子中微子。
因此,目前0号元素最主要存在于质量极大的中子星内部。正是这种高压的环境,该粒子才得以稳定存在。现阶段在常态环境下,我们很难探索0号元素的化学性质。
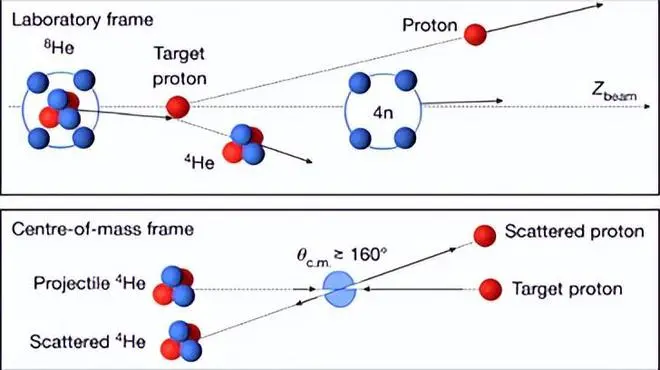
虽然我们无法在常态下得到中子,但在20年前,已有科学研究表明可能存在四中子的无电荷核系统。不过,当时的仪器设备误差较大,学界内对于该实验结果存在较大争议。
但是,随着科学技术的不断进步,近期已有报道称,四中子的无电荷核系统可以存在,这也是首次获得四中子核系统存在的确凿实验证据。目前,关于0号元素相关性质的研究仍处于探索阶段,这些研究将对于宇宙起源、亚原子结构等领域起到重要的推动作用。
问题来了,既然0号元素是存在的,那么会不会也存在其他元素周期表中所没有记录到的新元素呢?
元素周期表是否会新增元素呢?
原子核内部复杂的相互作用是原子核稳定存在的重要因素。根据计算,随原子序数的不断增加,以原子序数26的铁元素为界限,元素稳定性先增大后减小。也就是说,如果将所有元素排成一行的话,哪个元素距离铁元素越远,其稳定性就越差。
近代新元素的发现更多集中在原子序数大于110的超重元素,这些超重元素可以通过原子对撞的方式人工合成,具有放射性且寿命较短。2010年,117号元素被合成之后,元素周期表第七周期正式填满。之后十余年时间,科学家在对于第八周期元素的探索道路上从未停止脚步。
然而,由于超重元素的不稳定性,目前为止还尚未有第八周期的新元素被IUPAC承认。不过,研究人员表示,通过对微观粒子相互作用进行更系统的研究后,相信在将来可以提出新的合成方法,以实现到达超重元素“稳定岛”,构建第八周期元素。到那个时候,开辟元素周期表新纪元指日可待。
References
- Labarca M. An element of atomic number zero?[J]. New Journal of Chemistry, 2016, 40(11): 9002-9006.
- Marqués F M, Labiche M, Orr N A, et al. Detection of neutron clusters[J]. Physical Review C, 2002, 65(4): 044006.
- Duer M, Aumann T, Gernhäuser R, et al. Observation of a correlated free four-neutron system[J]. Nature, 2022, 606(7915): 678-682.
0 人喜欢
There is no comment, let's add the first one.