为什么可能没有体积的量子所组成的物质却有体积?
当你测量和观察周围的宇宙时,有一件事是可以肯定的:你看到、触摸到并以其他方式与之互动的物理对象都占据了一定的空间体积。无论是固体、液体、气体还是物质的任何其他形态,它都需要消耗能量来减少任何有形物质所占的体积。
然而,看似矛盾的是,作为物质的基本成分,标准模型的粒子却根本没有可测量的体积;它们只是点粒子。那么,由无体积实体组成的物质如何占据空间,创造出我们所观察到的世界和宇宙呢?
让我们从我们熟悉的事物开始,一步步分解,直到我们深入到支撑我们存在的量子规则。最后,我们可以从那里开始逐步向上。

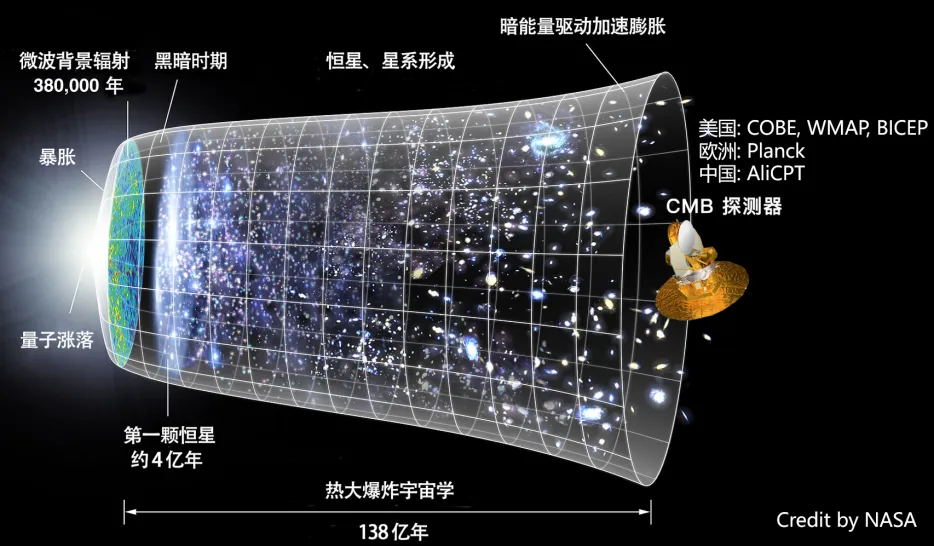
上图显示了对应于电磁波谱各个部分的尺寸、波长和温度/能量尺度。你必须使用更高的能量和更短的波长来探测最小的尺度。紫外线足以使原子电离,但随着宇宙的膨胀,光会系统地转移到更低的温度和更长的波长。
如果你想了解体积,那么你必须了解我们测量物体大小的方式。确定宏观实体大小的方式通常是将其与已知大小的参考标准进行比较,例如尺子或其他测量棒。或者测量弹簧(或类似弹簧的物体)因该物体而位移的力、测量光穿过物体跨度所需的传播时间,甚至通过用特定波长的粒子或光子撞击物体的实验反馈来进行确定。正如光具有由其能量定义的量子力学波长一样,物质粒子也具有等效波长——也就是它的德布罗意波长。
当我们分解物质本身时,我们会发现我们所熟悉的一切实际上都是由更小的成分构成的。例如,人类可以分解成各个器官,而器官又由被称为细胞的单个单位构成。一个成年人体内总共可能有 80 到 100 万亿个细胞,其中只有大约 4 万亿个细胞构成了您通常所认为的身体,包括您的肌肉骨骼系统、结缔组织、循环系统和所有重要器官。另外大约 40 万亿个是血细胞,而您体内有一半的细胞根本没有遗传物质。相反,它们是由单细胞生物(例如主要生活在肠道中的细菌)构成的;从某种角度来看,您的一半细胞甚至不是您!
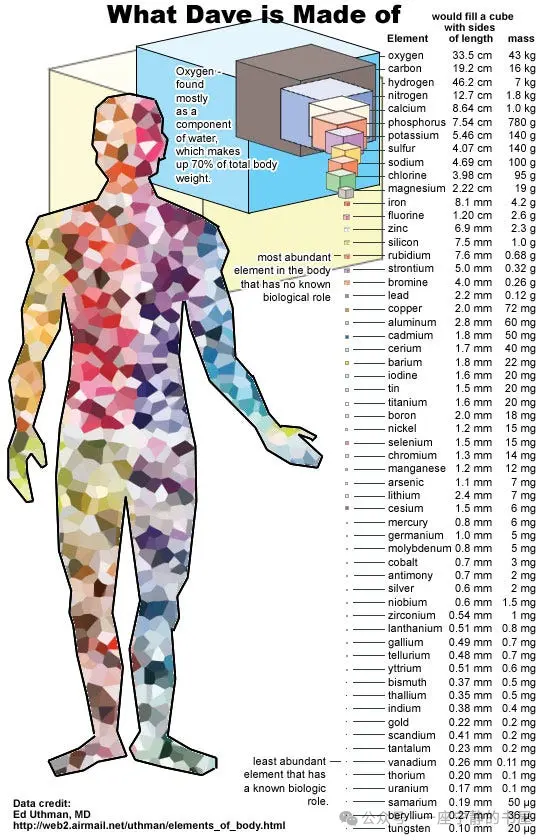
虽然人类是由细胞构成的,但从更基本的层面上讲,我们是由原子构成的。总的来说,人体内有近 10²⁸ 个原子,按数量计算主要是氢,但按质量计算主要是氧和碳。
细胞本身相对较小,通常只有约 100 微米左右,通常需要显微镜才能单独分辨。然而,细胞根本不是基本的物质单位,而是可以进一步分解成更小的组成部分。更复杂的细胞含有细胞器——执行特定生物功能的细胞成分。这些成分中的每一个又由分子组成,分子的大小从纳米级开始;单个 DNA 分子虽然非常细,但伸直后比人的手指还长!
而分子又由原子组成,原子的直径大约只有一埃,通常具有球对称性,在三个维度上具有相同的尺寸。在 19 世纪的很长一段时间里,人们都认为原子是基本粒子;原子这个名字本身就意味着“无法切割”。但后来的实验表明,原子本身是由更小的成分组成的,包括电子和原子核。即使在今天,电子也无法分解成更小的成分,但原子核毕竟具有有限的尺寸,它们通常只有几飞米的直径,存在于比原子本身小约 100,000 倍的距离尺度上。
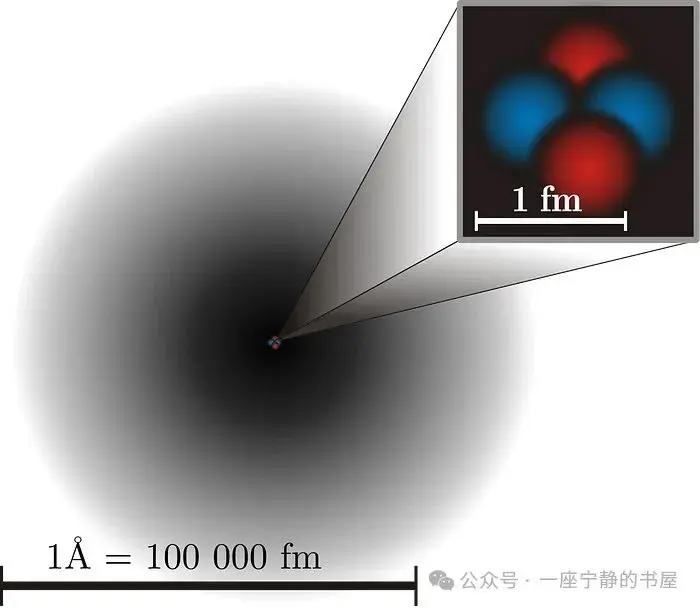
虽然从体积上看,原子大部分是空的,主要由电子云组成,但致密的原子核只占原子体积的 10¹⁵ 分之一,却包含原子质量的 ~99.95%。与局限于原子电子的跃迁相比,原子核内部成分之间的反应可以更精确,在更短的时间尺度上发生,并且能量也不同。
但原子核也不是基本粒子,它们是由更小的实体组成的。每个原子核由单个质子或质子和中子的混合物组成,单个质子(或中子)的直径经测量在 0.84 到 0.88 飞米之间。质子和中子本身可以进一步分解为夸克和胶子。最后,至少根据目前最好的实验和观察结果,我们终于知道了构成我们日常生活中接触的大部分正常物质的基本实体:电子、胶子和夸克。
涉及粒子对撞机的高能物理实验对这些基本粒子的大小施加了最严格的限制。得益于欧洲核子研究中心的大型强子对撞机,我们可以明确地说,如果这些粒子中的任何一个确实具有有限的尺寸,或由更小的成分组成,我们最强大的加速器和对撞机也无法将它们分解开来。它们的物理尺寸必须小于约 100 泽米,即 10^-19 米。
不知何故,构成我们所接触的一切事物的基本成分根本没有可测量的尺寸,表现为真正无量纲的点粒子,但它们结合在一起,却产生了我们在所有尺度上发现的全套实体:质子和中子、原子核、原子、分子、细胞成分、细胞、器官和生物。
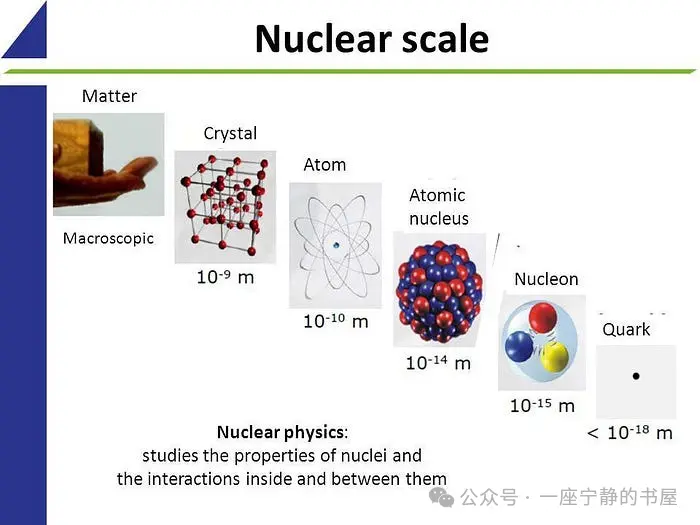
从宏观尺度到亚原子尺度,基本粒子的尺寸在确定复合结构的尺寸方面只起到很小的作用。这些构成块是否是真正的基本粒子或点状粒子仍不得而知,但我们确实了解宇宙,从大的宇宙尺度到微小的亚原子尺度。夸克和胶子的尺度是我们探索自然的极限。
那么这是如何实现的呢?点状粒子(可能尺寸无限小的粒子)如何结合在一起形成具有正的、有限的、非零尺寸的物理对象?
这有三个方面,这三个方面都是理解我们周围的宇宙所必需的。
首先,存在一条量子规则——泡利不相容原理。它阻止任何两个特定类型的相同量子粒子占据相同的量子态。粒子有两种,费米子和玻色子,虽然对于在同一物理位置可以占据相同量子态的相同玻色子数量没有限制,但泡利不相容原理适用于所有费米子。鉴于每种夸克和每个电子都是费米子,这条规则甚至排除了无限小的粒子在同一空间体积中共存。仅基于这条规则,你就可以看到多个粒子,即使它们本身没有“大小”,也需要彼此相隔有限的距离。
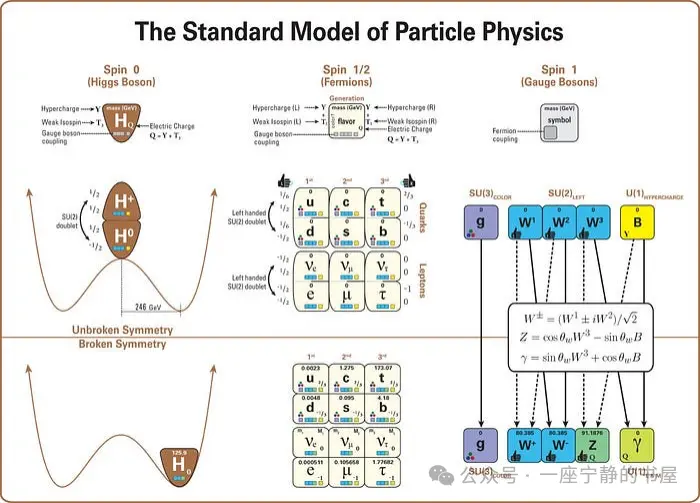
该图显示了标准模型的结构(与基于 4×4 粒子正方形的更熟悉的图像相比,它更完整、更少误导地显示了关键关系和模式)。具体来说,该图描绘了标准模型中的所有粒子(包括它们的字母名称、质量、自旋、手性、电荷以及与规范玻色子的相互作用:即强力和电弱力)。它还描绘了希格斯玻色子的作用和电弱对称性破坏的结构,表明希格斯真空期望值如何破坏电弱对称性以及其余粒子的性质如何因此而改变。但中微子的质量仍未得到解释。
第二个方面是这些粒子具有固有的基本属性,这些属性包括电荷、弱同位旋和弱超电荷以及色荷等。具有电荷的费米子粒子(受泡利不相容原理影响的粒子)将受到电磁力,与光子耦合。具有弱同位旋和弱超电荷的费米子粒子会受到弱核力,与 W 和 Z 玻色子耦合。而具有色荷的费米子粒子会受到强核力,与胶子耦合。
事实证明,夸克和电子(以及电子的两个较重的基本表亲,即介子和τ粒子)都带有电荷,这意味着它们都经历了电磁相互作用。在电磁学中,同性电荷(++ 或 - -)排斥,而异性电荷(+- 或 - +)吸引,物体越接近,力就越强。所有夸克都具有色荷,这意味着它们都经历了强核力。强核力总是具有吸引力,但表现方式不太直观,在粒子间距非常小的情况下,强力会变为零,但两个带色荷的物体之间的距离越远,强力就会增强。如果两个复合物体总体上是色中性的,但由具有色荷的实体(如质子和中子)组成,它们会表现出所谓的残余强力,这种力会吸引附近带有色荷成分的物体,但随着它们之间距离的增加,这种力会很快降至零。
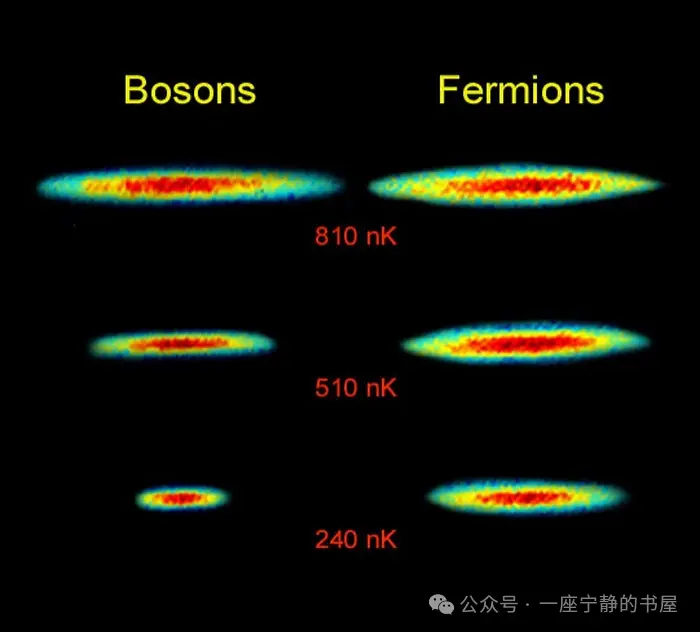
泡利不相容原理阻止两个费米子在同一个量子系统中以相同的量子态共存。然而,它只适用于费米子,如夸克和轻子。它不适用于玻色子,因此,可以在同一量子态中共存的相同光子的数量没有限制。这就是为什么含有费米子的恒星残骸,如白矮星和中子星,可以抵御引力坍缩,因为泡利不相容原理限制了有限数量的费米子可以占据的体积。
同时,所有基本费米子都具有某种类型的弱电荷(同位旋或超电荷),但考虑物体的大小时可以安全地忽略这种力。
最后,决定宇宙中物体大小的第三个因素是宇宙中所有费米子(和一些玻色子)固有的另一个基本量子属性——质量。如果一个物体没有质量,即其质量为零,那么它就不能保持静止,而是必须始终保持运动,而且必须以宇宙中允许的最快速度——光速来运动。光子没有质量,胶子没有质量,引力波也没有质量。它们都可以携带能量,但没有固有质量,因此,它们总是以允许的最大速度运动。
值得庆幸的是,宇宙中有许多实体确实具有质量,包括所有夸克、电子和电子的(较重的)近亲:μ 子和 τ 粒子。电子是极轻的粒子,而夸克的重量范围从“比电子稍重”(上下夸克)到“已知最重的基本粒子”(顶夸克)。拥有质量意味着粒子的移动速度低于光速,甚至能让它们在适当的条件下静止下来。如果没有夸克和电子的巨大性质,以及赋予这些粒子质量的希格斯场,这些物体(如质子、原子核、原子)以及随后由它们构建的一切将完全不可能形成束缚态!
强力之所以能发挥作用,是因为存在“色荷”和胶子交换,强力是将原子核结合在一起的力。这种力由大量胶子的交换控制,速度受光速限制;从黑洞视界内部来看,这样的力不可能阻止任何外层粒子到达中心奇点。
牢记这三个方面:
· 没有两个相同的费米子可以在同一位置占据相同的量子态,
· 粒子带电荷,这些电荷决定了它们所受力的类型和大小,
· 有些粒子具有有限的、正的、非零的静止质量,
我们最终可以开始用无限小尺寸的组成部分构建特定的、有限尺寸的物体。
让我们从质子和中子开始吧!它们是由夸克和胶子组成的实体。每个质子和中子内的夸克都带有电荷和色荷。相似夸克(上-上或下-下)之间的电力会引起排斥,而不同夸克(上-下-上)之间的电力会引起吸引力。当夸克彼此非常接近时,强力可以忽略不计,这意味着如果它们彼此靠近,它们会简单地“滑过”彼此。然而,它们相距越远,它们之间的吸引力就越大,从而阻止它们相距太远。事实上,一旦质子或中子内的夸克彼此达到临界分离距离,强力就会使它们“弹回”彼此,就像拉长的弹簧一样。
由于质子和中子中的夸克具有非零质量,这些夸克必须始终以低于光速的速度移动,从而使它们能够在这种复合结构中加速、减速,甚至(暂时)静止。夸克之间的强力和电磁力结合起来,产生了有限大小的质子和中子——每个略小于 1 飞米。而由于强力的作用,夸克之间的结合能最终成为质子和中子总质量的大部分。质子/中子的质量只有约 1% 来自其内部的夸克,而其余约 99% 来自这种结合能。
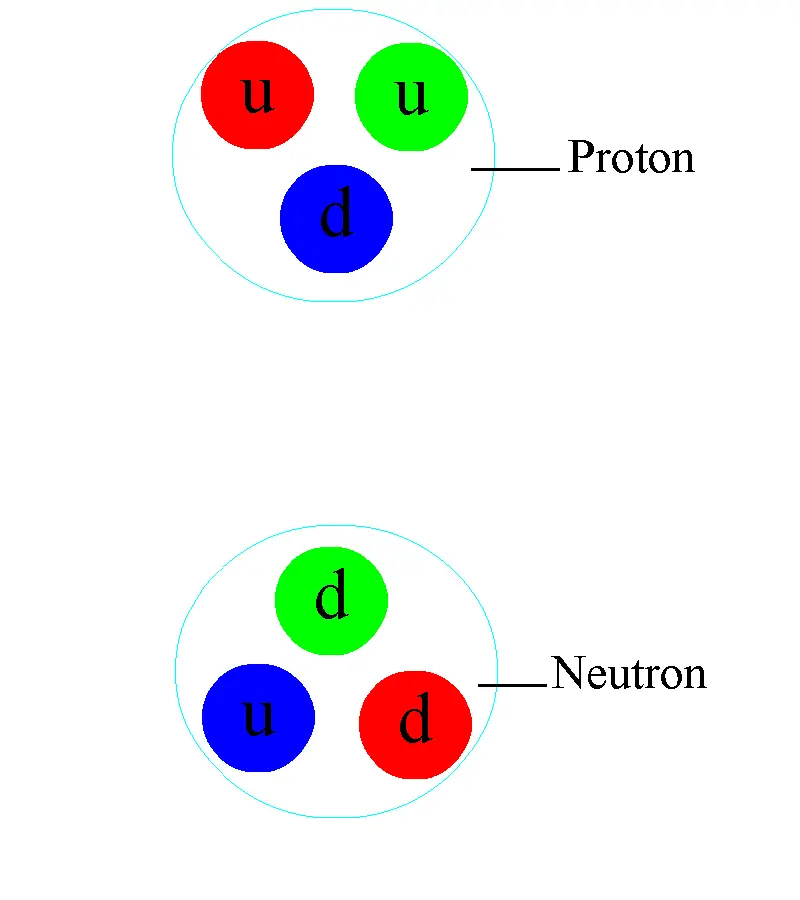
单个质子和中子是无色实体:这是当今宇宙中唯一允许存在的夸克态。虽然强力是由无质量(胶子)粒子介导的,但单个束缚态之间存在的唯一力是由介子引起的,介子本身都非常大,严重限制了强力的范围。
原子核稍微简单一些,原子核的体积大约等于其组成质子和中子的总体积。但对于原子本身(电子围绕的原子核)来说,事情就变得有点棘手了。电磁力现在是决定原子大小的因素,因为带正电、质量大的原子核锚定原子,而带负电、质量小得多的电子围绕原子核旋转。由于它们彼此带有相反的电荷,原子核和电子总是相互吸引,但由于每个质子的质量是每个电子的 1836 倍,所以电子会围绕每个原子核快速移动。毫不奇怪,最简单的原子是氢原子,其中只有一个电子围绕一个孤立的质子旋转,由电磁力结合在一起。
现在,记住泡利不相容原理:没有两个相同的费米子可以在同一位置占据相同的量子态。氢原子很小,因为它的电子处于允许的最低能量状态,即基态,并且只有一个电子。然而,较重的原子核(如碳、氧、磷或铁)在其原子核中含有更多质子,因此需要其中有更多的电子。如果较低能量的量子态都充满电子,那么后续电子必须占据更高能量的状态,从而导致更大的电子轨道(平均而言)和占据更大体积的“更蓬松”的原子。每个碳原子有六个电子,氧原子有八个,磷原子有十五个,铁原子每个有二十六个电子。
原子核心的质子越多,原子外围的电子就越多。电子越多,必须占据的能态数量就越多。原子中最高能电子的能态越高,原子必须占据的物理体积就越大。氢原子的直径可能只有约 1 埃,但较重的原子可能大得多,直径可达数埃。
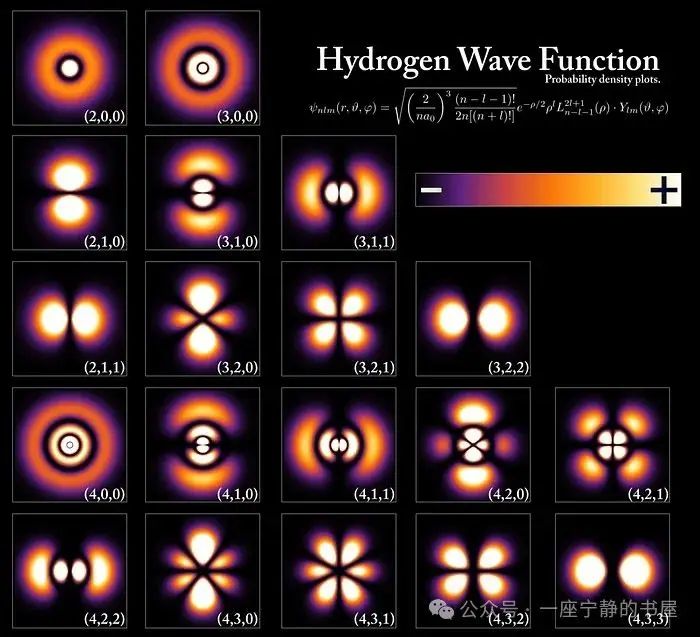
氢原子中不同状态对应的能级和电子波函数,尽管所有原子的配置都极为相似。能级以普朗克常数的倍数量化,但轨道和原子的大小由基态能量和电子质量决定。根据泡利不相容原理,只有两个电子(一个自旋向上,一个自旋向下)可以占据每个能级,而其他电子必须占据更高、体积更大的轨道。当你从较高能级降至较低能级时,如果你只打算发射一个光子,你必须改变你所处的轨道类型,否则你将违反某些无法打破的守恒定律。
尽管原子经常会聚集形成更大的结构,但大多数物体所占的体积主要可以通过了解物体组成原子本身所占的体积来解释。原因很简单:泡利不相容原理指出,没有两个相同的费米子可以占据相同的量子态,它阻止相邻原子的电子侵占另一个原子所占的体积。以人类为例,我们主要由碳、氧、氢和氮组成,其余大部分由磷、钙、铁和其他中等重元素组成。考虑到一个典型的成年人体内大约有 ~10²⁸ 个原子,如果你假设一个典型的原子的边长约为 ~2 埃,那么对于一个成年人来说,这相当于大约 80 升的体积:大约相当于一个体重 ~180 磅(80 公斤)的成年人的体型。
当然,在特殊情况下,这些规则可能会略有不同。例如,在白矮星中,许多原子聚集在一个位置,以至于围绕原子核运行的电子实际上被周围的压缩引力压垮,迫使它们占据比正常情况小得多的体积。在μ子原子中,原子的电子被电子的较重表亲μ子取代,原子的直径仅为电子原子直径的 1/200,因为μ子的质量大约是电子的 200 倍。但对于构成我们熟悉经验的传统物质来说,这是以下因素的累积效应:
· 电子的质量较低但不为零,
· 电子的强负电荷,
· 以及质量巨大、带正电的原子核,
· 结合泡利不相容原理,
正是这些因素决定了原子以及地球上所有物体所占据的体积。从基本的量子实体一直到我们生活的宏观世界,这就是从根本上来说微小的物体,甚至可能是点状物体最终占据如此大空间的原因!
--------------------------------------------
本文转载自公众号一座宁静的书屋
0 人喜欢
There is no comment, let's add the first one.