如果一个人身体死了但大脑活在营养液中,是不是活在虚拟世界里?
在现代科幻电影的奇异世界中,常常会出现这样的场景:一个人的身体已经死亡,但大脑却被保存在营养液中,继续在虚拟世界里体验着生命。《黑客帝国》中的就是这样一种构想,人类的大脑通过电信号与计算机系统连接,生活在一个被编程的虚幻世界中。然而,这种幻想并非纯粹的娱乐创作,它也反映了人们对大脑与身体关系的深层思考。

哲学家希拉里·普特南提出的“缸中之脑”假想,把这种思考推向了极致。他设想了一个邪恶科学家通过手术将人的大脑取出,放置在营养液中维持生命,再通过计算机程序向大脑输入信息,制造出一个人工的虚拟现实。在这个假想中,被操作的大脑仍然可以体验到生活的一切,但所有的感知和记忆都可能是虚假的。这样的假想引发了一个问题:如果一个人的大脑被置于这样的环境中,那他或她是否真的活在虚拟世界里?

揭秘大脑的复杂运作机制
要探讨这个问题,我们需要从大脑的运作机制入手。每个人体内都存在着一个错综复杂的神经系统,这个系统由神经纤维构成,包括各种神经组织,如大脑和脊髓。这些神经组织负责将神经信号传递给身体的各个器官,同时也将各个器官的信号传递回大脑和脊髓。正是通过这样的信号传递,我们才能感受到外部世界的各种刺激,并做出相应的反应。
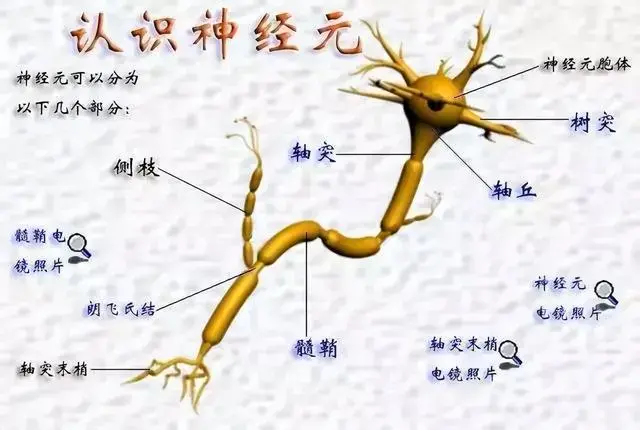
神经元是神经系统的基本单位,它们之间通过电信号进行通讯。当电信号在神经元之间传递时,会转变为化学信号,这种信号的转换是通过神经递质来完成的。我们的记忆、感知和反应都是基于神经元之间这种电信号和化学信号的交流。大脑的结构和运作方式在某种程度上类似于电脑,但它的效率和耗能方面远胜于电脑。这一点从大脑处理信息和储存信息的方式就可以看出。
因此,从理论上讲,如果能够维持大脑的电活性和化学平衡,就有可能保持大脑的正常工作状态。但这是否意味着大脑可以在脱离身体的情况下活在虚拟世界里呢?目前科学界的共识是,尽管理论上存在这种可能性,但以我们现有的技术还无法实现。大脑的构造极其复杂,我们对其了解仍然有限,尤其是对于每个神经元的具体功能,我们知之甚少。
虚拟世界:技术梦想与现实挑战
电信号在人类感知和记忆中扮演着至关重要的角色。我们的感觉、思考和记忆都是通过神经元间的电信号交流来实现的。基于这一点,科学家们开始尝试通过计算机程序来模拟人类的感知和记忆,这在某种程度上已经在人工智能和机器学习领域取得了一些突破。但要完全模拟大脑的工作方式,仍然面临巨大挑战。

在电影《黑客帝国》中,人类的大脑被用来作为人工智能的电池,通过电刺激来构建一个虚拟世界。虽然这种场景在现实世界中尚未实现,但它提出了一个有趣的问题:如果我们能够模拟大脑的电信号,是否就能创造出一个让人们生活在其中的虚拟世界?
目前,我们的技术还无法做到这一点。大脑中的神经元数量庞大,达到860亿之多,而且我们至今还不清楚每一个神经元的具体功能。因此,要完全模拟大脑,不仅需要了解每个神经元的功能,还需要找到能够模拟这种复杂网络的方法。尽管未来技术的发展可能会为我们打开新的可能性,但在当前阶段,“缸中之脑”的设想仍然遥不可及。
未来技术的伦理困境与生命思考
尽管“缸中之脑”在当前技术水平下还只是一个遥不可及的梦想,但它却为我们提供了一个思考未来科技可能性的窗口。随着神经科学和人工智能技术的不断进步,我们或许会对大脑有更深的了解,也许有一天,我们真的能够模拟出一个虚拟世界。

然而,这样的技术发展也带来了伦理上的担忧。如果一个人的大脑可以被操纵,记忆可以被篡改,那么个体的自我意识和自由意志又将何去何从?这些问题不仅是科学和技术的挑战,更是对我们社会伦理观念的考验。
在此基础上,我们不得不重新思考生命的意义。如果一个人可以在没有身体的情况下活在虚拟世界里,那么生命的本质是什么?我们的感知、记忆和意识是否只是大脑中的电信号和化学反应?这些深刻的哲学问题,可能需要我们每个人来共同探索答案。
0 人喜欢
暂无评论,来发布第一条评论吧!

