浅谈《天国：拯救》中的骰子游戏

原链接：

https://zhuanlan.zhihu.com/p/386924079?utm_campaign=shareopn&utm_medium=social&utm_psn=1806094671581167616&utm_source=wechat_session

正文：

《天国：拯救》是由战马工作室制作的中世纪RPG游戏，根据1403年发生的真实历史改编。本作的故事发生在中世纪时，匈牙利之王与瓦茨拉夫四世内战的波西米亚，《天国：拯救》的故事是根据真实历史改编的。随着贤君查理四世驾崩，神圣罗马帝国陷入了战争、腐败与混乱。

瓦次拉夫，查理四世的儿子，却沉迷荒淫之事而不理朝政。瓦茨拉夫不满的宗亲贵族最后只能求助于瓦茨拉夫的皇兄——匈牙利之王，西格斯蒙德。

但西格斯蒙德最后采用了极端的方式，绑架国王，逼其退位，趁乱夺权，其率部队大举进攻波西米亚，并侵蚀国王盟友的领地。

在这乱世中，铁匠之子亨利在城镇斯卡里茨和父母过着平凡而快乐的生活，但这平静生活被一群库曼人雇佣军所打乱，他们收到了西格斯蒙德的亲令，掠夺并烧毁了城镇，在这次混乱中，亨利是为数不多的逃过这场浩劫的幸存者之一。

游戏中玩家将扮演加入拉德季·科比拉阁下麾下的反抗军的亨利，在众人的帮助下追查杀害他父亲的雇佣兵头领，为其铁匠父亲报仇并夺回父亲的遗物——为拉德季大人铸造的宝剑。命运将他带入这场冲突中，以及这场决定波西米亚的未来的内战。

在游戏过程中，我们会在在任务中需要和NPC玩骰子赌博，也能在酒馆和旅店门前看到不时会有两个平民对坐在一张木牌桌上相互“切磋”。本文将以小见大，从《天国：拯救》的骰子游戏中挖掘西欧中世纪时期骰子游戏的经济学原理和历史溯源。

图片来源：《天国：拯救》艺术设定集

库曼人雇佣军

历史溯源：

骰子在五千年前西亚地区就有使用。最早期的骰子并非现在常见的正多面体，而是角锥或棒状的，正多面体的骰子是由牛或羊的距骨刻成。最早的骰子游戏可追溯至公元前3000年的古埃及文明，古埃及人在一个称为塞尼特（senet）的桌游中使用一种两面的骰子进行游戏。此外，古希腊人与古罗马人亦有用距骨作为骰子玩抛掷游戏的历史。玩法通常是将跖骨抛上，用手接下，同抓布包游戏一样考验小孩的神经反应。跖骨因能掷出四面，可作为骰子游戏，也被认为是六面骰的前身。

图片来源：www.lostkingdom.net

1个古埃及骰子及2个罗马骰子

中国的骰子习惯在一点和四点漆上红色，据清代赵翼考证红四点最早为唐玄宗所使用

而《天国：拯救》中的骰子游戏正是一种称为Farkle的骰子游戏。中世纪往往是指从公元5世纪罗马帝国分裂到公元15世纪文艺复兴的这段时期。而Farkle，据现今主流的说法，可能起源于14世纪，由冰岛的Albert Farkle爵士发明，后传到欧洲。首次关于Farkle的文字记载出现在莎士比亚时期。不过也有说法认为Farkle起源于美国西进运动时期，因为臼莓木（farkleberry）木质坚硬不易损坏而常被拓荒者用于制作骰子。Farkle自20世纪80年代起被注册商标多达6次，但现今的Farkle游戏来自于Legendary Games游戏平台。1996年Legendary Games平台更改了Farkle的传统的积分规则，并添加了部分新的计分规则，将其命名为“PocketFarkle”并于1997年发售。如今Farkle已是一种风靡欧洲的骰子游戏，战马工作室将其收录入《天国：拯救》也不足为奇了。

图片来源：战马工作室官方推特账号

游戏中Farkle规则

骰子游戏是中世纪社会的重要组成部分，在西欧中世纪时期欧洲地区，无论是市井小民，还是王公贵族，骰子游戏和纸牌桌游在人们的日常娱乐中同样享有举足轻重的地位。无论是在街头的酒馆，还是在贵族的牌桌，都能见到骰子的身影。除了Farkle外，还有很多其他种类的骰子游戏深受人们喜爱。

（阿拉伯语，意为骰子），流行于13世纪的欧洲，起源于阿拉伯和中东地区。被认为现代骰子游戏的鼻祖之一。游玩需要两枚六面骰子，玩家需从5到9中选一个数，比如玩家选择5，并投掷骰子3轮，如果掷出5，则玩家获胜，若3轮均没掷出为则轮到下一位玩家。下一轮中若玩家选择选择7，则投掷结果若为7则获胜，结果若与上一轮所选的数一致（5），则玩家出局。人数若较多的每人只能投掷一轮。

Glückshaus（德语，意为幸运之屋），流行于15-16世纪文艺复兴时期。常见于酒馆和商人间，是一种备受人们喜爱的赌博和消遣骰子游戏。游玩需要一块有编号为2-12的格子的专用游戏板和两枚六面骰子。在每个格子上至少放一枚硬币。若掷出3，5，6，8，9，10和11，且对应的格子有硬币，玩家则获得格子上的硬币，反之则需在格子中放置硬币。掷出7（婚礼）则在其中放置硬币，掷出2（猪）则可取走除7之外所有格子的硬币，掷出12（国王）则可取走包括7在内所有格子的硬币，掷出4则跳过。

图片来源：Wikipedia

Glückshaus游戏板

经济学原理：

介于不同地区和版本下，Farkle的规则稍微有些不同，比如在经典模式下加入了叫做cutthoat的模式，也就是说，当你本轮作废，也就是官方说法“Farkle”的时候，累积的分数将给对方。那么游戏中的Farkle又有什么不同呢？

先来介绍一下Farkle的规则

（1）玩家会在第一轮掷出所有的骰子

（2）每掷一轮，玩家至少要选出一枚骰子，选出的骰子必须要符合点数积分表的要求，并累积得分

（3）结束一轮投掷后，玩家可选择继续投掷或者停止并将累积分数。倘若投掷出的骰子都没有得分，则该轮作废，也叫做Farkle

（4）当玩家达到目标点数（如2000点）时，则获得胜利

积分表如下：

首先是出现了一些所谓的”作弊“手段，通过背景设定，游戏中的人都用自己的骰子，所以在自己的骰子中加些私货也就不足为奇了。在游戏中，使用不同性质的骰子会有不同的效果

例如

奇数骰子：容易出奇数的骰子

天国骰子：容易掷出1点和5点，会增加掷出连续骰子的概率

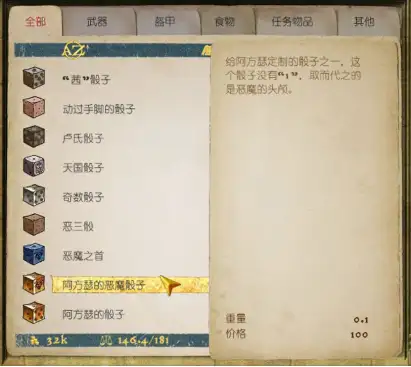
图片来源：游戏

部分特殊骰子

一般来说，从花花公子DLC中获得的阿方斯的恶魔骰子效果最佳

然而在与基友（bushi）现实中玩Farkle的时候（肯定不能像游戏一样作弊啊），如何把把分高让我苦苦思索。因而，为了寻找Farkle中的最优决策，我进行了以下探讨：

首先我们先大致看一下出现“得分组”的概率，1点和5点都是单个出现便可得分，概率都为1/6三个相同点数的概率为5/54,而其他组合概率看起来低的离谱

显然，通过加权平均数算出得分期望这条路难走。所以，介于编程能力的缺乏，之后的分析都是通过实验来证明。

玩Farkle有两个关键因素，第一是选得分骰子的决策，我把它称为”策略“。第二是什么时候停止投掷，我把它称为”止损“。（xs，好像原意有点不沾边）

现在，我决定我的策略为“有分就拿”，也就是说，投出骰子，拿走所有得分的组合。然后我们来探讨什么时候”止损“效果最佳。

当”止损“为三个骰子时，也就是说，如果一轮中拿完得分的骰子所剩的骰子小于等于三个，则停止投掷并计分。以下是实验结果：

当”止损“为两个骰子时，实验结果如下：

当”止损“为一个骰子时，实验结果如下：

加上之后我线下和基友做了多次实验，统计发现，“止损”为一个骰子时Farkle的次数太多，”止损“为三个骰子的时候得分均值小于”止损“为两个骰子。线下测试结果如下（以10000分为上限）。

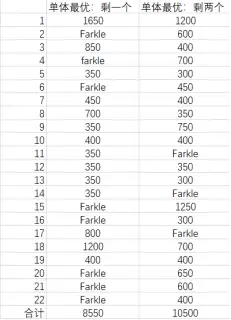
综上所述，当“止损”为两个骰子时，总体得分最高

现在我们来探讨”策略“，显然，有分就拿并不是最优“策略”，因为这样会丧失高得分组合的概率。经过多次尝试，我探讨出一种较为优势的“策略”

首先，我们需要确定一个期望值，如果在一轮投掷中得分的骰子没有达到期望值，则拿”单体最优“并进行下一轮投掷。

举个清晰的例子，比如说我的期望值是200，第一轮投掷出了153264，得分加总为150（一个1点、5点），没有达到我的期望值，所以我拿一个得分骰子，相比较1和5，1得分更高，所以拿”“单体最优”的1点，继续下一轮投掷。（附上重要的一点：”止损“的优先级高于”策略“）

因而，确定期望值的大小则需要我们去探讨

我先把期望值设在了200，以下是实验结果

除了极端值，发现均分都会在350上下波动

之后不同期望值下的结果是手写的，就不放到上面了。总之，期望值在200以上的得分总体没有太大差距，比期望值为150、和200的稍微高一些

设置期望值的主要目的是，尽量使高得分组合出现的概率增加，不然以”有分就拿“的策略，虽然确保了Farkle的发生概率低，但是平均得分较低。

所以，经过多次线上线下尝试，我总结出来的经验是： “止损”为两个骰子，采用”期望值“策略，期望值设定在200

其实Farkle这个游戏告诉我们，如何在一定风险的情况下做到收益最大。

”止损“的目的就是防止极端事件的发生，例如金融市场上的VaR。

“有分就拿”策略是牺牲较多风险换取较为稳定的低收益，好比在金融市场上购买债券，基金。

“期望值”策略则是牺牲较为稳定的低收益，以较高风险追求较高收益，好比在金融市场上购买股票。

结语

《天国：拯救》中的这款小游戏不仅能让你时不时从忙碌的各种主线支线，各种跑图中解放出来，在酒馆小酌几口，和赌棍们“切磋技巧”小赚几个格罗申，领悟了其中的原理还能帮你从现实生活中及时止损，小赚几个W。可谓是两全其美，真就玩着游戏就把钱赚了。当然，在现实生活中我们还是要杜绝赌博，遵纪守法。毕竟现实生活中可不能用几个格罗申就能把警察叔叔打发走的。

参考文献：

1. Dimitris Romeo Havlidis，MEDIEVAL GAMBLING GAMES: DICE & STREET GAMES，sociology,24/1/2017

https://www.lostkingdom.net/medieval-gambling-games-dice/

2. 百度百科，《天国：拯救》

https://baike.baidu.com/item/%E5%A4%A9%E5%9B%BD%EF%BC%9A%E6%8B%AF%E6%95%91/12806156?fr=aladdin

3. 维基百科，骰子

https://zh.wikipedia.org/wiki/%E9%AA%B0%E5%AD%90#%E6%AD%B7%E5%8F%B2

4. Wikipedia，Dice

https://en.wikipedia.org/wiki/Dice#History

5. The History of Farkle!，Farkle Fans，5/1/2012

http://farklefan.blogspot.com/2012/01/history-of-farkle.html

6. Jon G，BoardGameGeek，22/5/2007

https://www.boardgamegeek.com/thread/167091/article/1510621#1510621

7. Wikipedia，Glückshaus

https://de.wikipedia.org/wiki/G