买量平台大数据杀熟惯用手段以及应对策略
渠道会计算游戏的ROI杀熟吗?里讨论了,买量广告平台是否会计算游戏ROI杀熟,不少人感兴趣,今天展开讲讲。
答案是显而易见的,当然会。
广告平台本身也要追求利益最大化。
例如Facebook,99%收入来自于广告,23年底员工数量达67317人,产品、研发、平台等,按美国的工资可是不少一笔费用,这还没有算外包的广告审核、客服费用。
Google平台也类似,国内的几个平台一般是单独的产品变现部门,需要抗KPI,KPI一般是对于去年的收入增长比例。
追求业务增长,是这个时代精英们的共识。
1 点击计费到曝光计费&广告系统自动化
早期广告平台大多都还有根据click点击计费的选项,当市场地位持续巩固后,不约而同地转向了CPM计费,也是就按广告曝光收钱。
之前广告主可以根据流量质量好坏决定投放方式,通过一些投放技巧来规避垃圾版位,这是媒体最不愿意看到的。
因为自己变现的版位,有几个一直卖不出去,丧失了赚钱的机会。
最理想的是,每个广告版位,都可以卖出去,即便效果差挣的少一点,也比一分都不挣要好。
如果按点击计费,垃圾广告位可能会有很多曝光,但是没点击,这样收益是0。
改成曝光计费后,优质版位混合垃圾版位一起卖,这样你就可以理解为啥现在越来越多的广告平台,都越来越趋近于自动化投放了吧?
表面上买量平台会对外公开讲:为了减少广告账户多而导致的内耗,简化账户结构,增大机器学习占比,我们会用机器学习进行数据建模,辅助买量员提高工作效率,从而使投放效果更上一个台阶。
实际上买量平台变现负责人的目标是:优质流量混合垃圾流量一起打包竞价拍卖,让每个版位都可以最大程度变现;无限降低广告平台操作门槛,让更多人可以0门槛上手,从而全民竞价,进一步提高买量竞争程度,从而实现下个季度利润增长。
当然,买量平台会先把自己最优质的流量转变为CPM曝光计费,其他第三方软件接入SDK买流量给媒体变现的,仍是CPC计费,因为这部分作弊太多。
筛选非常严格的平台也有统一按曝光计费,不过缺点是增加了外部流量的监督成本。
由于国内几个媒体不单独披露广告收入变化,我用海外的举个例子:
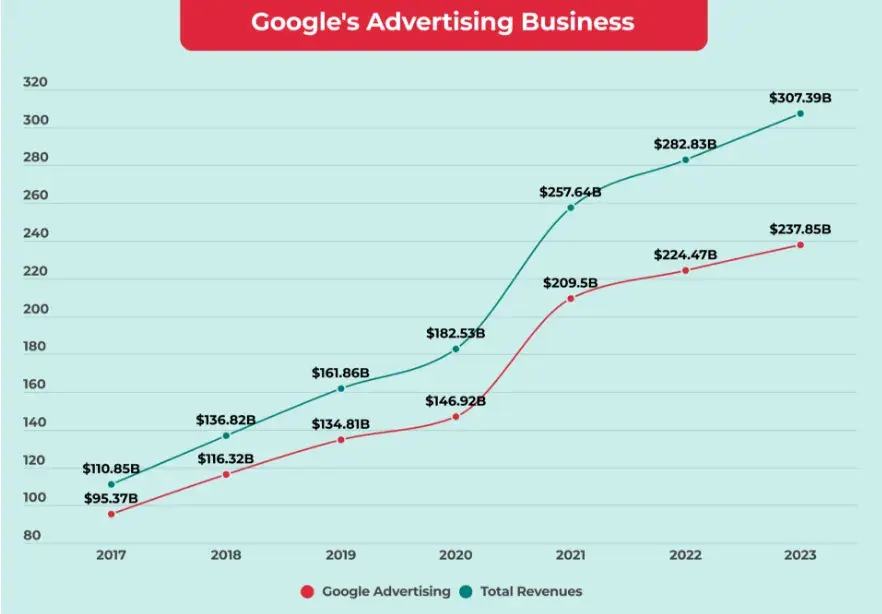
Google从2017年强制使用自动化投放系统UAC后,广告收入暴增。
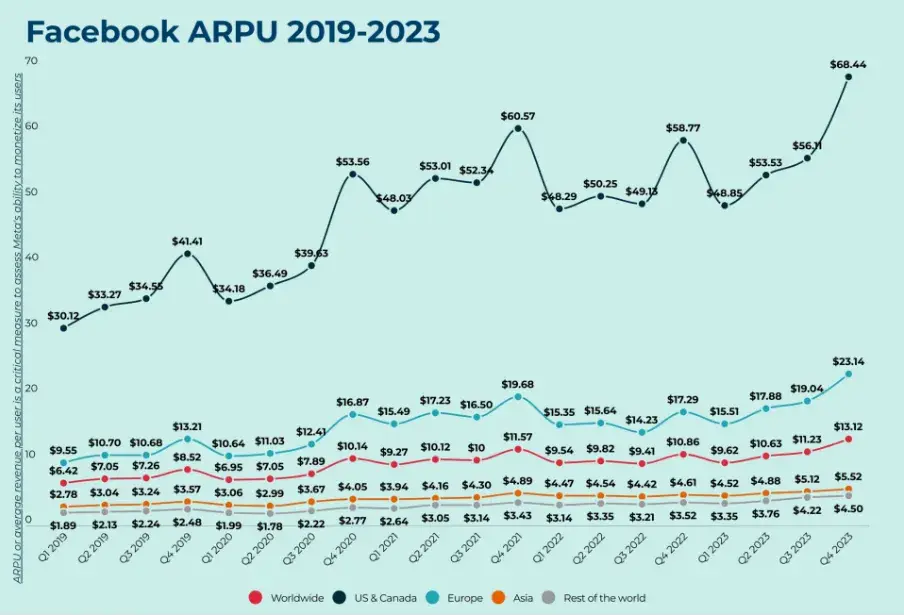
Facebook在2020年也推出自动化投放系统,不过不是强制选,其收入也在稳步上升。
当然买量平台收入上升不是单一因素,不过自动化系统绝对起着关键作用。
买量平台在推出新功能后,会用各种办法让你使用,给点免费广告费,再让客户经理疯狂宣传,力争让所有客户全都用上,从而提高平台自身收入。
这点国内字节巨量2.0,腾讯广点通3.0也在跟进。
强势媒体的收入增长手段,基本都比较类似,弱势媒体速度缓慢,本身用户质量不高,改完后广告主也不使用。
2 流量质量分层售卖
除了上面讲的,另外一个有效手段是,根据用户质量进行分层,出价高给好量,出价低给垃圾量。
没错,就是各个买量平台都在用的常规操作。
游戏APP来举例,买量平台上,广告投放目标分为安装、自定义事件(充值)、充值金额。
如果你投放目标选安装,会买来非常多用户,成本低,但是付费率不高,最终ROI基本不太可能回本。
如果投放安装就能回本,怎么让你投放出价更高、竞争更激烈的优质流量呢?
| 广告投放目标 | 成本 | ROI |
| 安装 | 低 | 基本回不了本 |
| 充值事件 | 偏高 | 付费率高,中小R多 |
| 充值金额 | 最高 | 付费率最高,大R多 |
从这个简单的表格就可以看出来,买量平台的流量根据质量分层,安装低成本卖给一些只要人头的,充值事件卖给充值内购类的游戏;
如果你想要大R,得掏更多钱来抢量。
跟打车软件根据用户使用安卓苹果手机,从而采取不同定价一个套路。
用户质量分层收费加上自动化投放系统,让强势买量平台收入持续上升。
更有甚者,如字节,不满足于只赚广告费,游戏厂商们的数据我都能看到,根据数据来做游戏。
既当裁判员,又当运动员,都来抢游戏这块肥肉。
苦逼的游戏厂商只能一边硬着头皮继续买,另一边开动聪明的小脑瓜,应对如此艰难的局势。
3 不负责任的奇淫技巧
华南国内买量厂商惯用套路是,卡付费回传。
第一种是648都不传,只传小额付费,控制出价中等偏上,确保能曝光到相对价值偏高的人群,同时控制付费事件的成本到游戏品类的大盘均值,避免被媒体发现利润率过高,闷声发大财。
这种模式,就好比告诉媒体,我能出有竞争力的价格抢量,但是付费都是小额玩家,让广告平台的算法多给你推一点好量,平台表面上不能太过分,你一直亏就会降预算,维持在合适比例的付费数据,让你不砍预算就行。
第二种是小额付费不传,只传128以上大额,大幅提升出价,去钓大R,因为出价不到一定高度,是无法持续曝光给大R人群的。
这种模式释放给媒体的信息是,我能承受极高的成本,务必曝光到头部高价值用户,适合养大R滚服的品类,一个服就靠一个大R就能收回来,其他都是陪玩小弟。
第三种是大额玩家分多次付费事件,回传给广告系统,甚至有些极度活跃的正向用户也可以穿一个首冲回去,但要控制在很低比例。
这种适合跑机器学习占比大的渠道,付费事件必须到一定数量才能维持住平台的买量模型,不够的多传一些,往上放量会更容易点。
最后,广告平台的策略也是一直在变的,所以很多方法时灵时不灵,但核心原理是不变的,需要买量员不懈探索。
-------------------------
转载自公众号游戏马可听,原文地址:买量平台大数据杀熟惯用手段以及应对策略
0 人喜欢
There is no comment, let's add the first one.