数学学习记录之重回代数拓扑
又是枯燥的一天,今天我重回代数拓扑,重新搞懂了一些以前不懂的东西。在这里我不得不吐槽一下,代数拓扑是真的难学,虽然这可能是因为我选的教材的原因,因为我更加喜欢内容简洁直奔主题的书,不喜欢总是废话一大篇的内容,不过这却更加增强了内容的抽象程度,也意味着更大的挑战。我看过几本关于代数拓扑的书,但目前我就在用Tammo Tom Dieck的Algebraic Topology这本书。
首先这本书是不适合初学者的,因为它需要一定的一般拓扑学的基础,而且如同我上面所说的一样,这本书作者说的话非常地精炼,加上基本上纯文字叙述,显得抽象性非常地高。同时,书本中的很多命题都没有证明,有些应该是结论的命题直接出现在正文的叙述中,默认读者已知。这无不给读者增添了难度。
重回主题,今天我学代数拓扑,在复习连通空间的过程中,遇到几个怎么想都想不懂的问题,然后我果断打开维基搜索connected space,并查阅其它书籍,发现我的问题跟connected space的两个命题有关,其中有个还没有证明。于是,我犹豫了几下,果断开始尝试自己证明,放弃去查找证明,就当作自己平时的练习吧。其实数学证明有时候是不需要动笔写的,直接脑子过一遍证出来就过了。不过这次我还是尝试写一写完整的证明,毕竟写论文的时候还是需要有完整的证明的,不会写就完蛋了。第一个命题,我花了一分钟左右就直接证完了,非常地简单,这有点出乎我的意料,因为写之前我几乎没有任何头绪。第二个命题我在证之前先自己写个类似的命题去证,结果最后一步卡住了证不出矛盾,于是我改回原来的条件,瞬间就证出来了。
其实正如Deligne所说:All the mathematical problems are psychological。所有的数学问题都是心理上的。遇到这两个命题时我毫无头绪,也不知如何下手。但接下来我克服心理障碍,尝试动笔去证出来,最后两个命题都用反证法给证出来了,整个过程行云流水,因为数学本就是自然的。所以,别再说什么学数学秃头了,学数学最大的困难就是心理障碍而已。
 图1 拓扑学关于连通性的两个命题的证明
图1 拓扑学关于连通性的两个命题的证明

图2 维基百科连通空间
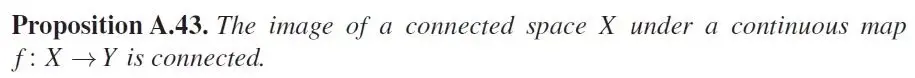 图3 连通空间的一个命题
图3 连通空间的一个命题
——————————————————————————
本文原于2020年9月1日 23:57发布于QQ空间
0 人喜欢
There is no comment, let's add the first one.

